Tweet                                                                            

Unlock the secrets behind AI! Discover why mastering the mathematical foundations of deep learning is the key to building innovative models and transforming industries. Ready to elevate your understanding of artificial intelligence? Dive into our comprehensive guide!

Mastering the mathematical foundations of deep learning, including vectors, matrices, linear algebra, calculus, and statistics, is essential for building effective AI models and navigating real-world applications, ensuring successful outcomes in various industries.

The Mathematical Foundation of Deep Learning: Your Complete Guide to Understanding AI

Imagine you are an architect about to design a magnificent skyscraper. Would you start building without understanding structural engineering? Of course not—the results would be catastrophic. Yet every day, countless developers dive into artificial intelligence projects without grasping the mathematical foundations that make deep learning possible. This approach is like performing heart surgery without knowing human anatomy: technically possible, but dangerously misguided.

The truth is, mathematics is not just an academic prerequisite for AI—it is the essential blueprint that shapes every model you will ever create, from conversational chatbots to strategic game-playing agents. Whether you are building recommendation systems that drive billions in e-commerce revenue or developing language models that transform how we interact with technology, your success hinges on understanding these fundamental mathematical concepts.

Why Mathematical Foundations Matter More Than Ever

In today’s AI landscape, the stakes have never been higher. Companies are investing billions in deep learning technologies, and the difference between success and failure often comes down to one critical factor: whether developers truly understand what is happening under the hood of their models.

Consider this real-world scenario: You are tasked with building a recommendation system for an e-commerce platform that serves millions of customers. Without understanding matrix multiplication, you will struggle to efficiently match customers to products.

Without grasping how gradients work, you will be lost when your model stops improving. Without statistical concepts like variance, you will find it impossible to explain prediction confidence to business stakeholders and assess risk.

These are not just theoretical concepts—they are practical tools that directly impact business outcomes and can mean the difference between a model that generates millions in revenue and one that fails spectacularly in production.

The Essential Mathematical Toolkit

Understanding Data Structures: Vectors, Matrices, and Tensors

Think of vectors, matrices, and tensors as the fundamental building blocks of all deep learning data structures. Just as architects need to understand materials like steel and concrete, AI practitioners must master these mathematical constructs.

A vector is simply a one-dimensional array of numbers—imagine a single row in a spreadsheet. In practical terms, a vector might represent daily stock prices over a week, features of a product, or the semantic meaning of a word in an embedding space. When you hear the term “word embedding” in natural language processing, you are talking about vectors that capture the meaning of words in mathematical form.

A matrix extends this concept to two dimensions, like a complete spreadsheet with rows and columns. In machine learning, a matrix might store a batch of word embeddings where each row represents a different word, or it could contain pixel intensities in a grayscale image.

Tensors represent the most powerful concept—they generalize vectors and matrices to any number of dimensions. Picture a stack of spreadsheets forming a three-dimensional cube, then imagine extending this to even more dimensions. This might sound abstract, but tensors are everywhere in AI. A batch of color images forms a four-dimensional tensor (batch size, height, width, color channels), while video data creates a five-dimensional tensor by adding time as another dimension.

Modern deep learning frameworks like TensorFlow 2.19 are built specifically for efficient operations on tensors of any shape or size. What makes this particularly exciting is the seamless integration with NumPy 2.0, which enables effortless interoperability between different mathematical libraries. This means you can leverage the strengths of multiple tools in unified, elegant workflows without the friction that once existed.

The Language of Transformation: Linear Algebra Operations

Once you understand how data is structured in tensors, the next crucial step is learning how to manipulate and transform that data. Linear algebra provides the essential toolkit for working with vectors, matrices, and tensors in deep learning. Matrix multiplication stands as perhaps the most fundamental operation in neural networks. This single operation underlies nearly every computation in deep learning models, combining input data with model weights to produce activations—the outputs of each neural network layer.

To put this in business terms, imagine you need to calculate sales totals across multiple products and regions. Instead of iterating through each combination individually, matrix multiplication lets you compute all combinations efficiently in a single step. This same principle applies when your neural network processes thousands or millions of data points simultaneously.

Other essential linear algebra operations include the dot product, which measures similarity between two vectors (a core concept in attention mechanisms used in modern language models), andtranspose operations, which swap rows and columns in matrices and are often necessary for aligning data dimensions correctly.

The Engine of Learning: Calculus and Optimization

While linear algebra helps organize and transform data, calculus drives the learning process itself. In deep learning, derivatives and gradients show how changing a parameter (like a weight or bias) affects the model’s performance.

Think of a gradient as a GPS system for optimization. Just as your car’s GPS constantly points toward your destination, gradients point in the direction of steepest improvement for your model. The gradient is essentially a collection of partial derivatives—a vector that tells you exactly how to adjust each parameter to minimize error.

This is particularly important in deep learning, where optimizing millions of parameters requires efficient computation of gradients at scale. The chain rule from calculus makes this possible by breaking down complex derivatives into manageable steps that can be computed automatically.

For example, when training a sentiment analysis model to understand customer feedback, gradients tell you precisely how to adjust thousands or millions of weights so the model better distinguishes between positive and negative reviews. The remarkable thing is that you do not need to calculate these derivatives manually—TensorFlow’s automatic differentiation system handles this complexity automatically.

This process of computing gradients and updating parameters lies at the core of model training.

It is how models learn from data, whether they are translating text, recognizing images, or learning to play games through reinforcement learning.

Probability and Statistics: Navigating Uncertainty

Machine learning inherently deals with uncertainty—data is noisy, patterns are imperfect, and predictions always carry some degree of risk. Probability and statistics provide the frameworks for modeling, quantifying, and reasoning about this uncertainty.

Consider building an email spam filter. Rather than simply labeling each message as “spam” or “not spam,” modern models predict probabilities—such as “90% likely to be spam.” This probabilistic approach reveals the model’s confidence and enables more nuanced handling of borderline cases and risk management. Probability distributions describe how likely different outcomes are in various scenarios. The Gaussian (normal) distribution, which forms the familiar bell curve, is widely used for modeling continuous data and initializing neural network weights. Categorical distributions handle discrete outcomes like email classification or predicting the next word in language models. Statistical measures like expectation (mean) and variance help you understand not just what outcomes to expect, but how much they might vary. In business contexts, high variance indicates less predictable results—potentially risky in domains like finance, healthcare, or autonomous systems. Understanding these measures helps you assess model stability and make safer, more reliable business decisions.

Neural Networks: Putting It All Together

Neural networks serve as the workhorses of modern deep learning, and they beautifully demonstrate how all these mathematical concepts work together. You can think of them as sophisticated information processing pipelines where each layer transforms data before passing it to the next layer.

A typical neural network contains three types of layers. The input layer receives raw data (such as a vector of word embeddings), hidden layers process data through learnable parameters called weights and biases, and the output layer produces the final prediction (such as class probabilities or regression values).

Weights determine how strongly each input influences neurons in the next layer—think of them as knobs controlling how much attention to pay to different input features. Biases are additional learnable parameters that shift the output, allowing the network to better fit the data. Both weights and biases are learned during the training process through the gradient-based optimization we discussed earlier. Activation functions introduce non-linearity into the network, enabling it to learn complex patterns beyond simple linear relationships. Popular choices include ReLU (Rectified Linear Unit), which outputs the input for positive values and zero for negative values, and softmax, which converts raw scores to probabilities that sum to one.

Without activation functions, neural networks would be limited to learning only linear relationships, regardless of their depth. It is the combination of linear transformations (matrix multiplication) and non-linear activation functions that gives neural networks their remarkable power to learn complex patterns.

The Learning Process: Loss Functions and Optimization

Training a neural network resembles learning to shoot basketballs. At first, your shots are scattered randomly, but with continuous feedback and adjustment, you gradually improve your accuracy. The loss function serves as your scorekeeping system—it quantifies how wrong the model’s predictions are compared to the actual targets.

Common loss functions include mean squared error for regression problems (measuring the average squared difference between predictions and targets) and categorical cross-entropy for classification tasks (measuring the difference between predicted probability distributions and actual class labels).

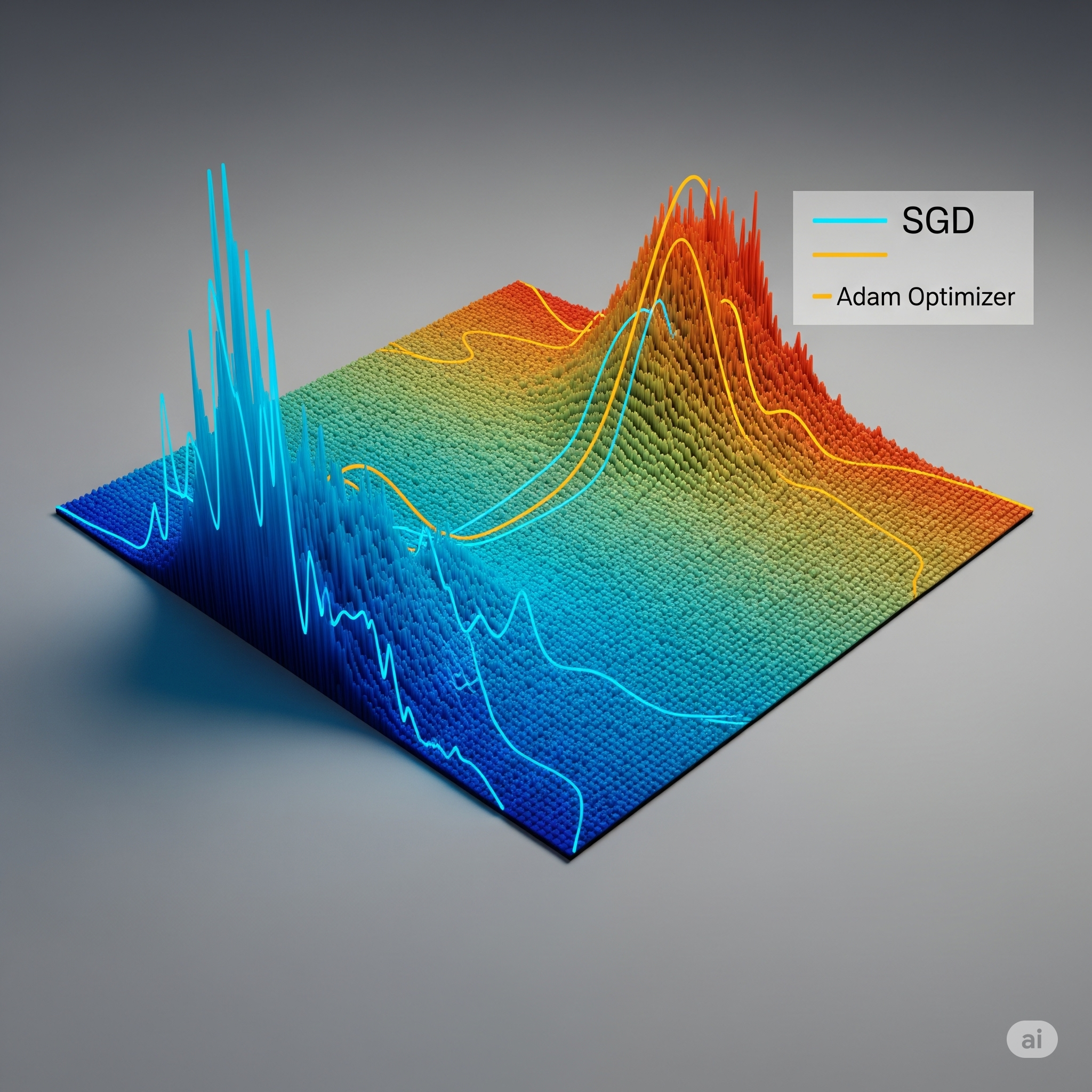
The optimizer is the algorithm that updates the model’s weights and biases to reduce the loss. Popular optimizers include Stochastic Gradient Descent (SGD), the classic approach that updates parameters in the direction of steepest descent, and Adam, an adaptive method that adjusts learning rates for each parameter and often converges faster than SGD.

Backpropagation is key to training neural networks. This algorithm uses the chain rule to efficiently compute gradients, enabling networks with millions of parameters to learn by tracking how each weight affects the final loss.

This process repeats over multiple iterations called epochs, with the model gradually improving its performance. Each epoch represents one complete pass through the entire training dataset, similar to reviewing all available training examples once before repeating to refine understanding.

Modern Considerations: From Theory to Production

Building an accurate model represents only the beginning of the machine learning lifecycle. In today’s environment, deploying, monitoring, and ensuring responsible use have become standard considerations in real-world machine learning practice. Model deployment involves taking your trained model and making it available for real-world use. TensorFlow models can be deployed to production using TensorFlow Serving for server and cloud environments, or TensorFlow Lite for mobile and edge devices.

Modern development environments provide powerful tools for deep learning experimentation and deployment. Google Colab offers free GPU and TPU access for rapid prototyping, while Amazon SageMaker provides end-to-end machine learning capabilities including notebook instances, distributed training, and production deployment with automatic scaling.

For local development, Jupyter Lab remains a favorite among data scientists, offering an interactive environment for code, visualization, and documentation. Visual Studio Code with its Python and Jupyter extensions provides a more IDE-like experience with integrated debugging and version control.

Cloud platforms like Google Cloud AI Platform, Azure Machine Learning, and IBM Watson Studio offer comprehensive environments for the entire machine learning lifecycle, from experimentation to production deployment with built-in monitoring and MLOps capabilities.

Amazon SageMaker includes essential features like data labeling, model training, hyperparameter tuning, and model deployment at scale. Their managed notebooks provide pre-configured environments with popular deep learning frameworks, while SageMaker Studio offers a comprehensive IDE for the entire machine learning workflow. The platform’s distributed training capabilities and automatic model optimization help reduce training time and improve model performance.

Additionally, Amazon Bedrock offers a fully managed service for building and scaling generative AI applications using foundation models. It provides seamless access to models from leading AI companies like Anthropic, AI21 Labs, Cohere, Meta, and Amazon’s own models. This complements SageMaker by enabling developers to integrate large language models and other foundation models directly into their applications without managing infrastructure.

Google’s equivalent offering is Vertex AI, which provides a unified platform for building, deploying, and scaling ML models. Vertex AI includes features for automated machine learning (AutoML), custom model training, and end-to-end MLOps. It also offers managed endpoints for model serving and monitoring, along with integration with Google’s foundation models through Vertex AI Model Garden.

Microsoft Azure’s Azure Machine Learning and Azure OpenAI Service provide similar capabilities. Azure Machine Learning offers comprehensive MLOps features, automated ML, and distributed training capabilities, while Azure OpenAI Service gives developers access to advanced language models like GPT-4 and DALL-E, along with fine-tuning capabilities and enterprise-grade security features.

Model monitoring becomes crucial after deployment. You need to track your models for performance degradation, data drift, or unexpected behavior. Tools like TensorFlow Model Analysis help detect issues before they impact business operations.

Responsible AI considerations include interpretability and fairness, which have become essential components of trustworthy AI systems. Libraries like SHAP (SHapley Additive exPlanations) provide techniques for understanding model decisions, while fairness analysis helps ensure your models work equitably across different demographic groups.

Your Path Forward

These mathematical foundations are not just academic exercises—they are your practical toolkit for solving real-world problems. The better you understand these concepts, the more creative and effective you will be in building AI systems that deliver genuine value.

Master vectors, matrices, and tensors, and you will understand how data flows through your models. Grasp linear algebra operations, and you will know how information gets transformed at each step. Understand calculus and gradients, and you will see exactly how your models learn and improve. Comprehend probability and statistics, and you will be able to reason about uncertainty and make better decisions.

When you encounter challenges in your AI projects—and you will—these mathematical foundations will be your guide. They’ll help you debug complex models when they behave unexpectedly, optimize performance when speed matters, design novel approaches when standard solutions fall short, and explain model behavior to stakeholders with confidence.

The journey from mathematical foundations to production AI systems might seem daunting, but remember that every expert was once a beginner. Start with these fundamentals, practice with real examples, and gradually build your expertise. The mathematical language of AI is learnable, and once you speak it fluently, you will have the power to build systems that can truly change the world.

Whether you are developing the next breakthrough in natural language processing, creating intelligent agents that make strategic decisions, or building any other form of artificial intelligence, these mathematical foundations will be your constant companions. Invest the time to understand them deeply, and they will serve you throughout your entire career in AI.

The future belongs to those who can bridge the gap between mathematical theory and practical application. By mastering these foundations, you are positioning yourself to be among the AI practitioners who do not just use the tools—but truly understand them.

About the Author

Rick Hightower brings extensive enterprise experience as a former executive and distinguished engineer at a Fortune 100 company, where he specialized in delivering Machine Learning and AI solutions to deliver intelligent customer experience. His expertise spans both the theoretical foundations and practical applications of AI technologies.

As a TensorFlow certified professional and graduate of Stanford University’s comprehensive Machine Learning Specialization, Rick combines academic rigor with real-world implementation experience. His training includes mastery of supervised learning techniques, neural networks, and advanced AI concepts, which he has successfully applied to enterprise-scale solutions.

With a deep understanding of both the business and technical aspects of AI implementation, Rick bridges the gap between theoretical machine learning concepts and practical business applications, helping organizations leverage AI to create tangible value.

Tweet                                                                            

comments powered by Disqus